Binary Tree – Searching a Node

An element in a binary search tree can be searched very quickly. A search operation on binary tree is similar to applying binary search technique to a sorted linear array. The element to be searched will be first compared with root node. If it matches with the root node then the search terminates. Otherwise search is continued in the left sub tree if the element is less then the root or in the right sub tree if the element is greater then the root.

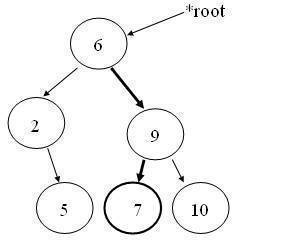
Suppose we try to find a node numbered 7 in it. First go down the right sub-tree (since value 7 is greater than the root value), and then go down the left sub-tree.

BST searchelement(BST *tree, int value) 
{ 
    if((tree->info == value) || tree==NULL) 
        return tree; 
    else if(value <tree-> info) 
        return searchelement(tree->left, value); 
    else 
        return searchelement(tree->right, value); 
} 

Finding the Smallest Node

Because of the property of binary search tree, we know that the smallest node in the tree will be one of the nodes in the left sub tree (if the left sub tree exists) otherwise root node itself will be the smallest node.

BST smallest(BST *tree) 
{ 
    if((tree == NULL) || (tree->left == NULL)) 
        return tree; 
    else 
        return smallest(tree->left); 
} 

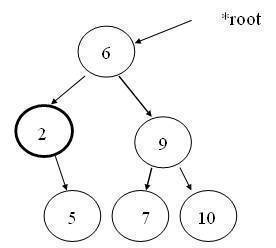
The above function returns a pointer to the node containing the smallest element in the tree. It does so, by tracing only the left side of the tree.

Finding the Largest Node

Because of the property of binary search tree, we know that the largest node in the tree will be one of the nodes in the right sub tree (if the sub tree exists) otherwise root node itself will be the largest node.

BST largest(BST *tree) 
{ 
    if((tree == NULL) || (tree->right == NULL)) 
        return tree; 
    else 
        return largest(tree->right); 
} 

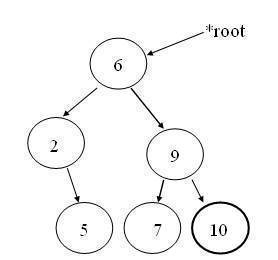
This function returns a pointer to the node containing the largest element in the tree. It does so, by tracing only the right side of the tree.