Trees

Arrays, linked lists, stacks and queues are used to represent linear and tabular data. These structures are not suitable for representing hierarchical data.

In hierarchical data we have

• ancestors, descendants
• superiors, subordinates, etc

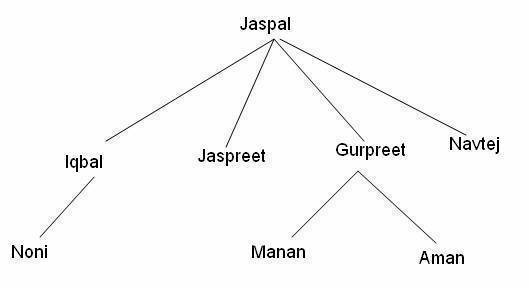
Family Structure

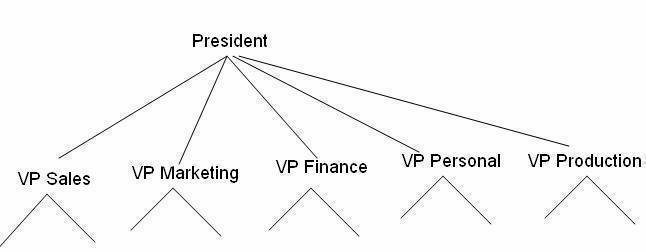
Business Corporate Structure

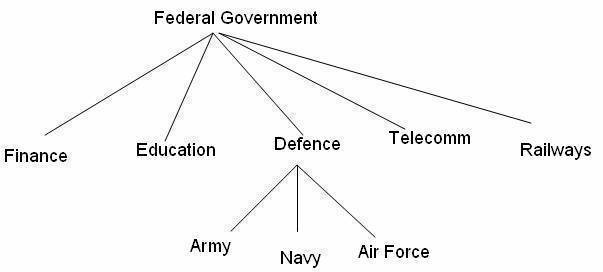
Federal Government Structure

Introduction to Trees

• Fundamental data storage structures used in programming
• Combine advantages of ordered arrays and linked lists
• Searching can be made as fast as in ordered arrays
• Insertion and deletion as fast as in linked lists

Tree characteristics

• Consists of nodes connected by edges
• Nodes often represent entities (complex objects) such as people, car parts etc.
• Edges between the nodes represent the way the nodes are related.
• It's easy for a program to get from one node to another if there is a line connecting them.
• The only way to get from node to node is to follow a path along the edges.

Tree Terminology

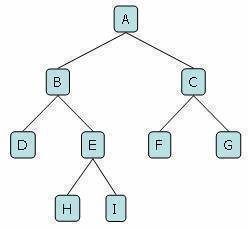
• Root: node without parent (A)
• Internal node: node with at least one child (A, B, C, F)
• External node: (a.k.a. leaf) node without children (E, I, J, K, G, H, D)
• Ancestors of a node: parent, grandparent, grand-grandparent, etc
• Depth of a node: number of ancestors
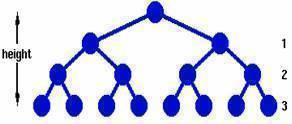
• Height of a tree: maximum depth of any node (3)
• Descendant of a node: child, grandchild, grand-grandchild, etc
• Degree of an element: no. of children it has
• Subtree: tree consisting of a node and its descendants

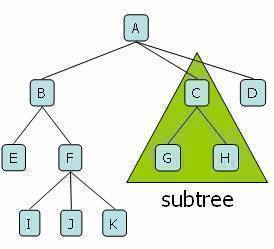
• Path: traversal from node to node along the edges that results in a sequence
• Root: node at the top of the tree
• Parent: any node, except root has exactly one edge running upward to another node. The node above it is called parent.
• Child: any node may have one or more lines running downward to other nodes. Nodes below are children.
• Leaf: a node that has no children
• Subtree: any node can be considered to be the root of a subtree, which consists of its children and its children's children and so on.
• Visiting: a node is visited when program control arrives at the node, usually for processing.
• Traversing: to traverse a tree means to visit all the nodes in some specified order.
• Levels: the level of a particular node refers to how many generations the node is from the root. Root is assumed to be level 0.
• Keys: key value is used to search for the item or perform other operations on it.

Binary Trees

• Every node in a binary tree can have at most two children.
• The two children of each node are called the left child and right child corresponding to their positions.
• A node can have only a left child or only a right child or it can have no children at all.
• A binary tree is a tree with the following properties:
  • Each internal node has at most two children (exactly two for proper binary trees)
  • The children of a node are an ordered pair
• We call the children of an internal node left child and right cild
• Alternative recursive definition: a binary tree is either
  • a tree consisting of a single node, or
  • a tree whose root has an ordered pair of children, each of which is a binary tree
• Applications:
  • arithmetic expressions
  • decision processes
  • searching

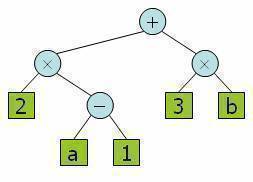
Arithmetic Expression Tree

• Binary tree associated with an arithmetic expression
  • internal nodes: operators
  • external nodes: operands
• Example: arithmetic expression tree for the expression (2 * (a – 1) + (3 * b))

Compiling arithmetic expressions

We can represent an arithmetic expression such as

(A + B) * (C + D) * 2 – X / Y as a binary tree, in which the leaves are constants or variables and the nodes are operations: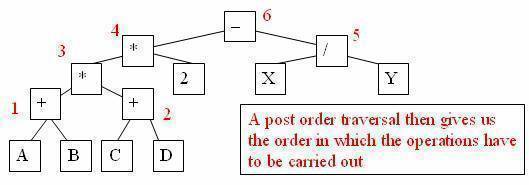

Properties of Proper Binary Trees

Notation

• n number of nodes
• e number of external nodes
• i number of internal nodes
• h height

Properties

• e = i +1
• n =2e -1
• h <= i
• h <= (n -1)/2
• e <= 2h