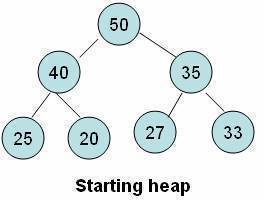
Deleting an Element from a Heap

Deleting an Element from the Heap

• Deletion always occurs at the root of the heap.
• If we delete the root element it creates a hole or vacant space at the root position.
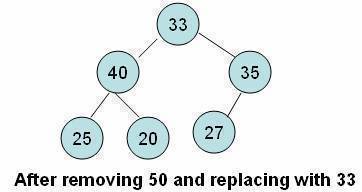
• Because the heap must be complete, we fill the hole with the last element of the heap.
• Although the heap becomes complete, i.e. it satisfies the shape property, the order property of heaps is violated.
• As the value that comes from the bottom is small, we have to perform another operation to satisfy the order property.
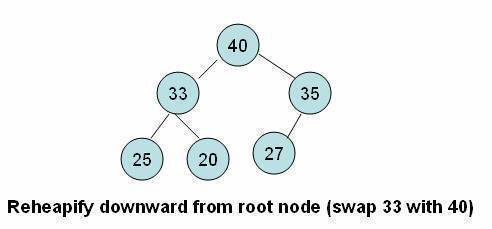
• This operation involves moving the element down from the root position until either it ends up in a position where the order property is satisfied or it hits a leaf node.
• In this tutorial, we refer to this operation as the reheapify downward operation.

Algorithm

ReheapifyDownward(heap,start,finish)

Here heap is a linear array, start is the index of the element from where the reheapify downward operation is to start, and finishis the index of the last element of the heap. The variable index is used to keep track of the index of the largest child.

Begin if heap[start] is not leaf node then set index=index of the child with largest value if(heap[start]<heap[index]) than swap heap[start] and heap[index] call ReheapifyDownward(heap,index,finish) endif endif end

C/C++ Implementation

.cf { font-family: Lucida Console; font-size: 9pt; color: black; background: white; } .cl { margin: 0px; } .cb1 { color: green; } .cb2 { color: blue; }

void reheapifyDownward(int heap[],int start,int finish)

{

 int index,lchild,rchild,maximum,temp;

 lchild=2*start; /*index of the left child*/

 rchild=lchild+1; /*index of the right child*/

 if(lchild<=finish)

 {

 maximum=heap[lchild];

 index=lchild;

 if(rchild<=finish)

 {

 if(heap[rchild]>maximum)

 {

 maximum=heap[rchild];

 &nbp; index=rchild;

 }

 }

 if(heap[start<heap[index])

 {

 temp=heap[start];

 heap[start]=heap[index];

 heap[index]=temp;

 reheapifyDownward(heap,index,finish)

 }

 } 

}

Coding the Function for Deletion

Deletion from the heap is done through the following steps:

• Assign the value of the root to a temporary variable, which can be returned from the function for further processing.
• Bring the last element of the heap to the root node position.
• Reduce the size of the heap by one.
• Apply the reheapify downward operation from the root node.

DeleteElement(heap,n,item)

Here heap is a linear array representing a heap with n elements. This algorithm deletes the element from the root of the heap and assigns it to item (an output parameter). Note that the code assumes that the array index begins from 1 and ends at n.

Begin set item=heap[1] set heap[1]=heap[n] set n=n-1; call reheapifyDownward(heap,1,n) End

C/C++ Implementation

int deleteElement(int heap[],int *n)

{

 int temp;

 temp=heap[1];

 heap[1]=heap[*n];

 --*n;

 reheapifydownward(heap,1,n);

 return temp;

}