AES (Advanced Encryption Standard) is the currently employed specification for encrypting electronic data by the United States National Institute of Standards and Technology, or NIST. AES was selected as the U.S. standard for encryption of unclassified information in 2001 supplanting DES which had been the U.S. standards for a number of years (since 1977). AES is based on the Rijndael cipher that was developed by Belgian mathematicians Vincent Rijmen and Joan Daemen. Their proposal was evaluated by NIST during the AES selection process and has since been adopted by both the United States government and other worldwide organizations. AES is a symmetric-key algorithm which makes use of the same key for both decrypting and encrypting information.
AES Highlights
The Advanced Encryption Standard (AES) was first announced by NIST on November 26th, 2001 as U.S> FIPS PUB 197, or FIPS 197 for short. This announcement followed a five year process during which 15 designs for a new standard were evaluated before the Rijndael option was selected as the most suitable one for the government’s goals. On May 26th, 2002, AES officially became the U.S. federal government’s encryption standard after gaining approval by the U.S. Secretary of Commerce. There are a number of encryption packages available which leverage AES, and it is the first open and publicly approved cipher by the U.S. NSA (National Security Agency) for use with top secret information when employed in a NSA-approved cryptographic module. The name of the algorithm, Rijndael, is a combination of the two inventors last names. The published AES standard is actually a variation of the Rijndael algorithm with a block size restricted to 128 bits.
How Does AES Work?
The AES algorithm relies on a substitution-permutation network and operates quickly in both hardware and software implementations. Deviating from the DES architecture, AES does not use a Feistel network. It has a fixed block size of 128 bits and the key size can vary between 128, 192, or 256 bits. The pure Rijndael algorithm does permit block and key sizes that may be any multiple of 32 bits to include a minimum of 128 and maximum of 256.
The AES cipher uses a 4 x 4 column, major order matrix of bytes that is called the state. Other versions of the Rijndael algorithm use a larger block size and can have additional columns in the “states.” The majority of AES calculations are conducted in a special finite field. The key size that is used; however, will dictate the number of repetitions of transformation rounds that will convert the plaintext or input, into the ciphertext. The total number of required cycles are:
10 repetition cycles for 128-bit keys.
12 repetition cycles for 192-bit keys.
14 repetition cycles for 256-bit keys.
Every round of AES will have a number of processing steps that include five stages. One of the stages will depend on the actual AES key itself. There is also a set of reverse rounds that are used to transform ciphertext back into plaintext using the same encryption key.
AES Description
The following are the high-level steps that the AES cipher takes when encrypting or decrypting data.
1 – KeyExpansion—During KeyExpansion, the AES round keys are derived from the cipher key using the Rijndael key schedule.
2 – InitialRound –
AddRoundKey—Each byte of the state is combined with the round key using bitwise xor.
3 – Rounds
SubBytes—AES uses a non-linear substitution step taking each byte and replacing it with another one based on a lookup table.
ShiftRows—AES uses a transposition step here. Each row of the state is shifted a certain number of steps cyclically.
MixColumns—In the MixColumns step, AES conducts mixing operation on the columns of the state. During this step, the four bytes in each column are combined.
AddRoundKey
4 – Final Round (Using no MixColumns)
SubBytes
ShiftRows
AddRoundKey
How Does the AES SubBytes Step Work?
During the AES SubBytles step, every byte in the state is fully replaced by using an 8-bit lookup table, also referred to as the 8-bit substitution box or the Rijindael S-box. This step provides the non-linear substitution in the cipher providing its strength. The S-box is derived from the multiplicative inverse over GF(28) which has been proven to have good, non-linear properties. To help avoid attacks based on simple algebra, the S-box is created by combining the inverse function with an invertible affine transformation. The S-box selection also makes sure to avoid any fixed points or opposite fixed points.
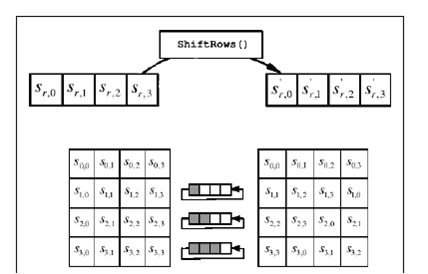
How Does the AES ShiftRows Step Work?
During the AES ShiftRows step, the bytes in every row of the state are cyclically shifted to the left. The number of places of the shift will differ for each row. In AES, the first row is not changed. In the second row, they are shifted by one to the left, two to the left in the third row, and so on. When dealing with data blocks sized 128 or 192, the shifting pattern remains the same. For Row n, the shift is left by n-1 bytes. This allows every column of the output state of ShiftRows to be made up of bytes from each column of the input state. For larger block sizes in the algorithm (but not the standard), the shift offsets differ.
For a 256 bit data block, the first row will be unchanged. The second, third, and fourth rows will shift by one, three, and four bytes respectfully. This modification in the shift is only applicable for implementations of the Rijndael cipher outside of the AES standard (AES does not use 256 bit data blocks). This step helps ensure columns do not become linearly interdependent.
The AES MixColumns Step
During the AES MixColumns step, every column of the state is multiplied by or with a fixed polynomial, c(x). They are combined by using an invertible linear transformation. MixColumns takes four bytes as its input and provides four bytes for output. Each input byte will impact all four output bytes. When combined with ShiftRows, MixColumns helps provide diffusion in the AES cipher.
During the MixColumns step, every column is multiplied by the known matrix for the 128 bit key.
Every column is treated as a polynomial over GF(28),and is then multiplied modulo x4+1 with a fixed polynomial c(x) = 0x03 · x3 + x2 + x + 0x02. The resulting coefficients are displayed in the hex equivalent of the binary representation of the bit bit polynomials from GF(28).
How Does the AES AddRoundKey Step Work?
During the AES AddRoundKey step, every byte of the state will be combined with a byte of the round’s subkey using an XOR operation. The subkey is combined with the state after being derived from the primary key using the Rijndael key scheduler. Every subkey is the same size as the state and is added by combining every byte of the state with the corresponding byte of the subkey using the bitwise, XOR operation.
Optimization of the AES Cipher
For computing systems that use 32 bit or larger words, the execution of AES can be increased by combining the SubBytles and ShiftRows steps with the MixColumns step. This is accomplished by transforming the steps into sequences of table lookups. To do this, four, 256 entry 32 bit tables are required and it makes use of 4096 bytes (four kilobytes) of memory (1 x kilobyte per table). This allows a round to be accomplished using only 16 table lookups and 12 23 bit XOR operations followed by 4 32 bit XOR operations in the AddRoundKey step. If the four kilobyte table is too large for the target platform, the table lookup operation can be accomplished using a 256 entry 32 bit table through the use of circular rotates. By using a byte-orientated approach, the steps can be combined into a single round for one operation.
AES Security
For the first eight years of the AES standard, the only attacks publicized against the standard used side-channel attacks against very specific implementations of the standard. While the Rijndael cipher was undergoing review, the NSA stated that it was secure enough for use on non-classified, U.S. government data. In the summer of 2003, the U.S. Government announced that AES was vetted for use on classified information at levels up to Top Secret. For use on Top Secret information, key lengths of 192 or 256 were required, and the system using the encryption had to be reviewed and certified by the NSA prior to being used.
Known AES Attacks
When attempting to break ciphers, any advantage that results in gaining time over a brute force attack is considered to be a “cryptographic break.” When dealing with theory, these advantages do not have to necessarily be achievable with the current computing technology of today. The most successful brute force attack against block-cipher encryption was against a 64 bit, Rc5 key by distributed.net in 2006.
In 2002, a theoretical attack against AES called the “XSL attack” was announced. Nicolas Courtouis and Josef Pieprzyk announced that they had discovered a weakness in the AES algorithm due to its basic description. Since that time, the XSL attack has been proven to be unworkable in practice.
Several years later on July 1st, 2009, Bruce Schneier wrote about conducting a related-key attack on the 192 and 256 bit versions of AES. This attack was reported to be discovered by Alex Biryukov and Dmitry Khovratovich. During the attack, the AES key schedule is the focus and only had a complexity score of 2119 at the time. In December of that year, it was improved to 299.5.
Also in the summer of 2009, a new attack by Alex Biryukov, Orr Dunkelman, Nathan Keller, Dmitry Khovratovich, and Adi Shamir was written about. During this attack against AES-256, there were two related keys used and it took 239 time to complete the 256 bit key of a 9 round version and 245 time for a 10 round version, and 270 time for an 11 round version. Since 256 bit AES makes use of 14 rounds, the attacks are not considered effective against a full AES implementation.
In the fall of 2009, the first AES known-key distinguishing attack against an 8 round version of AES-128 was released. The known-key distinguishing attack built on the rebound or start-from-the-middle attacks used on AES-similar permutations. During these attacks, the two consecutive rounds of permutation are viewed through the use of a Super S-box. The attack works on the 8 round version of AES-128 with a time complexity score of 248 and memory score of 232.
The next summer, in July 2010, Rijmen published a paper using chosen key relations in the middle attacks against AES-128. The first key recovery attacks against AES were published in 2011 by Andrey Bogdanov, Dmitry Khovratovich, and Christian Rechberger. This attack is faster than a brute force attack by approximately a factor of 4.
AES Side Channel Attacks
An AES side channel attack does not attack the cipher. Instead, this type of attack focuses on the implementation of AES on systems that can or will leak information. Since AES became the U.S. Government standard, there have been a number of attacks against various implementations of AES using these methods.
In the spring of 2005 (April 2005), a cache-timing attack against AES was announced by D. J. Bernstein. During this attack, he was able to break a custom server using OpenSSL AES encryption. The attack required access to more than 200 million plaintexts and the custom server was setup to provide as much timing information as possible. If the server were to not provide timestamps in its responses, the attack could still be carried out by timing the responses to and from over a significant number of sample messages being collected.
During November of 2010, Endre Bangerter, David Gullasch and Stephan Krenn published a practical way to achieve almost real time recovery of secret keys from AES-128. This method did not require either plaintext or ciphertext. Instead, the attack was based on the implementations of AES-128 that used compression tables similar to OpenSSL. This attack requires the ability to execute unprivileged code on the system that conducts the AES encryption. This can be achieved through the use of computer malware to gain access to the root account on the targeted system.
Nicolas Courtois maintains an excellent web page on the current state of attacks on AES.



Follow Us!