The Diffie-Hellman key exchange was first published by Whitfield Diffie and Martin Hellman in 1976 and is a popular method for exchanging cryptographic keys. The method is one of the most straight-forward examples of key exchanges implemented in the cryptology field and allows two individuals or parties that have not worked together before to establish a shared secret key over an insecure communications channel such as the Internet. Once the key is exchanged, the two parties can then use it to exchange encrypted information through the use of a symmetric key cipher.
Diffie-Hellman Key Exchange Background
The Diffie-Hellman key exchange scheme was originally proposed in 1976 in public. The methodology had been previously invented within the British Signals Intelligence Agency by Malcolm J. Williamson, but was kept classified at the time. 26 years after Diffie and Hellman published their original work, Hellman went on record to suggest a change in the naming of the algorithm to be Diffie-Hellman-Merkle key exchange to recognize the contribution of Ralph Merkle’s work to public key cryptography. Despite the original Diffie-Hellman key agreement being a non-authenticated key agreement protocol, it has provided the basis for a number of authenticated protocols since its publication. It is now used to help provide secrecy in TLS (Transport Layer Security) ephemeral modes that are known as DHE or EDH based on the cipher suite being used. Shortly after the publication of Diffie-Hellman, RSA was created that included an implementation of PKI that used asymmetric key algorithms.
How Does the Diffie-Hellman Key Exchange Work?
The Diffie-Hellman algorithm takes two systems parameters referred to as variables “p” and “g.” Each of the parameters are in the public and can be seen or used by all users in the given system. “P” is a prime number and the “g” parameter is referred to as the “generator.” “G” is normally an integer value that is less than “p.” Additionally, “g” will have an additional property or, for all numbers “n” that are between 1 and p-1 inclusive, there will be a power of the variable “k” of g that n = gk mod p.
An example exchange of a shared secret key using Diffie-Hellman would be similar to the following: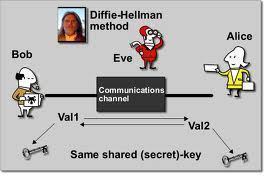
Step 1 – Person A will create a random private value, a. Person B will generate a random private value,b.
Step 2 – The random values created will be from the set of all integers.
Step 3 – Person A and B will then derive public values using the parameters p and g and their private values.
Step 4 – Person A’s public value will be calculated by using ga mod p, and Person B’s will be gb mod p.
Step 5 – Person A and B now exchange their public values.
Step 6 – Person A will calculate the secret key through the formula gab = (gb)a mod p, and Person B will use gba = (ga)b mod p. Since gab = gba = k, each person will now have the shared key, k.
The Diffie-Hellman protocol relies on the discrete logarithm problem for the overall security of the key exchange. The algorithm assumes that it is computationally infeasible to calculate the shared key given the two public values if the prime number used is large enough.
Diffie-Hellman Vulnerabilities
The Diffie-Hellman protocol is considered secure against others listening in or eavesdropping on communications as long as the variables are chosen appropriately. In this case, an eavesdropper would have to solve the overall Diffie-Hellman problem to obtain the shared key which is considered extremely difficult to accomplish. If a non-prime number, or small prime number is used in the algorithm, then the Pohlig-Hellman algorithm can be used to obtain a or b. As a result, a Sophie Germain prime number, q, is many times used to calculate p=2q+1 and is referred to as a “Safe prime” number. This label comes from the fact that the order of G is only able to be divided by q and 2. In this case, g is then selected to help create the order q subgroup of G instead of G. This helps prevent ga from revealing the lower order bit of a.
In addition to the weakness of using a weak random number generator without a completely random output, the traditional Diffie-Hellman key exchange algorithm does not provide a mechanism for authentication of communication between the two parties. As a result, it is vulnerable to the “man-in-the-middle” attack. This attack allows an imposter to pretend to be the desired party to each person entering into a key exchange. Once authenticated to each, this person can decode the traffic sent between each person.
Man-in-the-Middle Attack
As stated, one of the largest vulnerabilities to the original Diffie-Hellman key exchange algorithm is the main-in-the-middle attack. More explicitly, during this attack, a third party will intercept Person A’s public value, and then send their own public value to Person B. When Person B sends their public value, the third party will intercept it, and send along their own value to Person A. Once the agreement with each party is completed, the third party acts as an intermediary between them will full access to any messages sent to or from Persons A and B. Additionally, the third party has the ability to modify any messages sent from one party to another. This vulnerability exists primarily from the lack of identity authentication in the traditional Diffie-Hellman algorithm.
Mitigating the Man-in-the-Middle Attack
In order to defeat the main-in-the-middle attack, the STS (Station-to-Station) protocol was created by Diffie, van Oorschot, and Wierner in 1992. The protocol is also referred to as an authenticated Diffie-Hellman key agreement. In order to achieve the immunity to the attack, the protocol uses digital signatures and public key certificates. Generally, STS works like this:
Step 1 – Prior to executing the Diffie-Hellman key exchange, Person A and Person B obtain a public / private key pair and a certificate for their respective public key.
Step 2 – Once executing the protocol, Person A will computer a signature on some of the messages which covers the public value ga mod p. Person B will proceed in a similar fashion.
Step 3 – Although the third party is able to intercept messages between Person A and B, they are not able to forge signatures for either person without access to either Person A or B’s private key.
Other uses for Diffie-Hellman
Password Authenticated Key Agreement
Another use for the Diffie-Hellman algorithm is the password authenticated key agreement. In this scheme, Person A and B will share a password using a PAKE (password-authenticated key agreement) version of the Diffie-Hellman algorithm. This agreement is used to help prevent the man-in-the-middle attack. There are a number of ways to implement PAKE. One of the most common is to use the variable g, as the password. Another feature of this version of Diffie-Hellman, is that a third party is only able to test a single password on each iteration with one of the intended recipients. As a result, the modified system is able to provide a decent level of security without requiring strong or hardened passwords
Public Key Infrastructure
Diffie-Hellman can also be used as part of public key infrastructure today. In this scheme, the public key is used to prevent main-in-the-middle attacks. Since Diffie-Hellman is not used to sign digital certificates; however, RSA is used more commonly as the public key algorithm of choice in industry.
Creating and Exchanging Diffie-Hellman Keys in C++
Just about any programming language that provides support for cryptology libraries will also include support for creating and exchanging Diffie-Hellman keys. Although the following examples are based on the C++ programming language for Windows environments, they are similarly implemented in other popular programming languages.
How to Generate Diffie-Hellman Keys in C++
Similar to other major programming languages which support cryptography, the C++ development libraries for the Windows operating system (OS) allow developers to generate and share Diffie-Hellman keys. The following are the steps to generate a Diffie-Hellman key in C++
Step 1 – Use the CryptAcquireContext function to acquire a handle to the Diffie-Hellman Cryptographic Provider.
Step 2 – Select the method that you want to use to generate the new key. There are two ways to accomplish this in C++. First is to use the CryptoAPI to generate all of the required values for G,P, and X. Alternatively, you can use the existing values for G and P and generate a new value for X.
Step 3 – Then, use the CryptGenKey function and pass either the CALG_CH_EPHEM (ephemeral) or the CALG_DH_SF (store and forward) variables in the Algid parameter. The Diffie-Hellman key will then be created using the new, and random values for both G and P for the newly calculated value of X. The handle of the value will then be returned in the phKey parameter.
Step 4 – Your new key will be ready for use. At this point the values of both G and P have to be sent to the intended recipient along with the key when conducting a key exchange.
Steps to Generate Diffie-Hellman Keys using Predefined Values
C++ also allows one to generate Diffie-Hellman keys by using predefined values for both G and P.
Step 1 – Invoke the CryptGenKey function by passing either CALG_DH_EPHEM(ephemeral) or CALG_DH_SF (store and forward) in the Algid parameter. You also use CRYPT_PREGEN for the dwFlags parameter. This will generate a key handle that is returned via the phKey parameter.
Step 2 – Next, initialize a CRYPT_DATA_Blob structure with the pbData member assigned to the P value. The BLOB should contain zero header data and the pbData member will be in little endian format.
Step 3 – Call the CryptSetKeyParam function and pass the key handle that is retrieved earlier in the hKey parameter. The KP_P flag should be passed in the dwParam parameter, and a pointer to the structure containing the value of P should be passed in the pbData parameter. This will assign the value of P.
Step 4 – Create and initialize a CRYPT_DATA_BLOB structure that has the pbData member assigned to the G value. The BLOG will not contain any header data and the pbData member will be in little endian format.
Step 5 – Call the CryptSetKeyParam function and pass the key handle that was previously retrieved in the hKey parameter. Pass the KP_G flag in the dwParam parameter, and send a pointer to the data structure which includes the value of G in the pbData parameter of the function to set the value of G.
Step 6 – Generate the value of X by calling the CryptSetKeyParam function. The key handle that was previously retrieved should be passed in the hKey parameter and the KP_X flag should be passed in the dwParam parameter. Finally, the pbData parameter should be assigned a value of NULL when invoking the function.
Step 7 – Once the function call is complete, the Diffie-Hellman public key will be ready to use.
How to Destroy Diffie-Hellman Keys in C++
Once a Diffie-Hellman key is no longer needed, it should be destroyed. The following are the steps to do so in C++ for Windows computers.
Step 1 – Pass the key handle to the CryptDestroyKey function. If you previously specified CALG_DH_SF in earlier function calls, the key values are saved or persisted in storage with every previous call to CryptSetKeyParam. G and P values are able to be retrieved with the CryptGetKeyParam function.
Step 2 – Some CSPs will use hard-coded values for G and P. In these cases, you can expect to throw a NTE_FIXEDPARAMETER error if the CryptSetKeyParam is invoked with either KP_P or KP_G included in the dwParam parameter.
Step 3 – If you invoke CryptDestroyKey, the handle to the key will be destroyed; however, the key values will be maintained in the CPS. If you specified the value of CALG_DH_EPEM, then the handle to the key will be destroyed as well as all values being cleared from the CSP.
How Do You Exchange Diffie-Hellman Keys?
In order to exchange Diffie-Hellman keys, both of the parties have to agree to the parameters to use in the algorithm. These include P (a prime number) and G (generator number). In order to prepare a Diffie-Hellman public key to transmit to another party in C++, the following steps must be taken:
Step 1 – Invoke the CryptAcquireContext function to acquire a handle to the Microsoft Diffie-Hellman Cryptographic Provider.
Step 2 – Initiate or create a Diffie-Hellman key by invoking the CryptGenKey function. This will create a new key. Alternatively, you can invoke the CryptGetUserKey function to access or retrieve an existing key.
Step 3 – Acquire the necessary size to store or hold the Diffie-Hellman key BLOB through invoking the CryptExportKey function. This function should pass NULL in the pbData parameter. The pdwDataLen parameter will have the required size passed back through it.
Step 4 – Allocate sufficient memory for the Diffie-Hellman key blob.
Step 5 – Call the CryptExportKey function passing the PUBLICKEYBLOB in the dwBlobType parameter and your handle to the Diffie_hellman key in the hKey parameter to create a Diffie-Hellman public key BLOB. This function will force the calculation of the public key value.
Step 6 –The Diffie-Hellman public key BLOB is now ready to be further encoded and transmitted for use.
How to Import a Diffie-Hellman Public Key and Calculate the Secret Session Key
Another common task in cryptography using the Diffie-Hellman algorithm is the import of a public key and calculating the Secret Session Key. The following are the steps to do so in C++.
Step 1 – Invoke the CryptAcquireContext function to acquire a handle to the Microsoft Diffie-Hellman Cryptographic Provider.
Step 2 – Call the CryptGenKey function to initiate the creation of a new Diffie-Hellman key. Alternatively, you can invoke the CryptGetUserKey function to retrieve an existing key.
Step 3 – Import the Diffie-Hellman public key into the CP by invoking the CryptImportKey function. In the parameters of the function, you will need to pass a pointer to the public key BLOB in the pbData parameter. Additionally, the BLOB’s length will need to be passed in the dwDataLen parameter and the hPubKey parameter will contain a handle to the Diffie-Hellman key. These actions will result in the creation of the shared, secret key and complete the DH key exchange. The function will then return a handle to the secret key session in the hKey parameter.
Step 4 – Make the key usable by converting it to a session key type. To do so, invoke the CryptSetKeyParam function. In the function, the dwParam variable should be set to KP_ALGID and pbData assigned to a pointer to the ALG_ID value representing the session key. The key has to be converted before using the shared key in either the CryptEncrypt or the CryptDecrypt functions. The session key will now be ready for use in either decryption or encryption operations.
Steps to Export a Diffie-Hellman Private Key
Step 1 – Invoke the CryptAcquireContext function in order to obtain a good handle on the Microsoft Diffie-Hellman Cryptographic Provider.
Step 2 – Make a Diffie-Hellman key through invoking the CryptGenKey function for obtaining a new key. Alternatively, you can invoke the CryptGetUSerKKey function to access an existing key. Then, make a new Diffie-Hellman private key BLOB by invoking the CryptExportKey function.
Step 3 – The PRIVATEKEYBLOB value should be passed in the dwBlobType parameter and the handle to the Diffie-Hellman key should be passed in the hKey parameter of the function.
Step 4 – Once the handle to the key is not required, one should invoke the CryptDestroyKey function to destroy the key function.



Follow Us!