Angular acceleration is the rate of change of a body’s angular velocity compared to time. It is considered a vector quantity since it has a direction and magnitude. Angular acceleration is similar to linear acceleration except that it travels on an arc. Scientifically, it is equal to (final angular velocity – initial angular velocity) / time. A body’s angular velocity is the rate of change of angular distance with respect to time and acceleration is the rate of this change over the same time frame.
How is Angular Acceleration Measured?
Step 1 – Note the starting and stopping angular velocities for the object being measured.
Step 2 – Record the time it takes for the object to go from a cold start to the final angular velocity.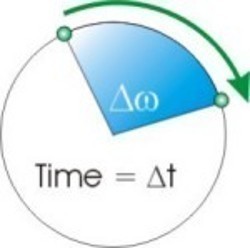
Step 3 – Subtract the initial angular velocity from the final to determine the total change in the object’s angular velocity.
Step 4 – Convert the angular velocity to the same time unit as the time period being used for the calculation. For example, if a propeller or saw’s angular velocity is expressed in revolutions per minute, but the measurement’s time period is in seconds, multiply the total RPMs by 60 to set the measurement to the right time period.
Step 5 – Divide the change in angular velocity by the total acceleration time. The result is the object’s angular acceleration.
How to Determine Revolutions from Angular Acceleration
An object’s revolutions over a given time period can be determined if the angular acceleration is known. The equation for motion of constant acceleration, x(t) = x(0)+v(0)t+0.5at^2, also has the angular acceleration equivalent: ?(t) = ?(0)+?(0)t+0.5?t^2. ?(t) represents the measurement of an angle at a time “t” and ?(0) refers to the angle at time zero. ?(0) is the initial angular speed at time 0 and ? is the constant angular acceleration. A common problem that occurs is determining the number of revolutions of a body after a time frame, t, when there is a constant amount of angular acceleration with a constant torque.
Step 1 – To determine the number of revolutions of a car wheel after 10 seconds with torque of 0.5 radians per second-squared, and an initial angular velocity of 0, enter the values in the angular acceleration equation to solve for ?(t).
Step 2 – Enter ?(0)=0 for the equation’s starting value and the following information will be available at this point: ?(10) = 0 + 0 + 0.5×0.5×10^2 = 25 radians.
Step 3 – Convert the radians result to revolutions by dividing ?(10) by 2?. This result is 25 radians / 2? = 39.79 revolutions.
Step 4 – Determine the distance the wheel traveled by multiplying the wheel’s radius by the result to finish the calculations.


Follow Us!